集合

定义

把研究的对象集在一起构成集合。

集合中

有有限个元素：有限集

有无限个元素：无限集

空集

不含元素的集合：Ø

空集也是有限集。

元素和集合的关系

属于：∈

不属于：∉

集合中元素的三个特征

1. 确定性：给定的集合，它的元素必须是确定的. 也就是说，给定一个集合，那么任何一个元素是否存在这一个集合中就确定了.

2. 互异型：一个给定集合中的元素是互不相同的. 也就是说，集合中的元素是不重复出现的.

3. 无序性：给定集合中的元素是不分先后的，没有顺序的.

数集

数学里最常用的集合是各种数的集合，简称数集。

示例

数集之间的关系（Venn 图）

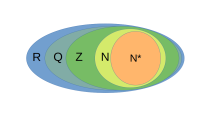
所有正整数组成的集合称为正整数集，记作 N*，Z₊ 或 N₊

所有负整数组成的集合称为负整数集，记作 Z_-

全体自然数组成的集合称为自然数集，记作 N

全体整数组成的集合称为整数集，记作 Z

全体有理数组成的集合称为有理数集，记作 Q

全体实数组成的集合称为实数集，记作 R

集合的表示方法

列举法

把集合中的所有元素一一列举出来，并用花括号“{ }”括起来表示集合的方法叫做列举法.

注意事项：

1. 元素与元素之间必须用“,”隔开.

2. 集合中的元素可以是任何事物.

3. 集合中的元素不能重复.

示例：

一元二次方程 3x²-6x=0 的解集为：{0, 2}.

描述法

一般地，设 A 表示一个集合，把集合 A 中所有具有共同特征 P(x) 的元素 x 所组成的集合表示为 {x∈A|P(x)}，这种表示方法称为描述法.

注意事项：

1. 写清楚集合中元素的符号. 如数或点等.

2. 不能出现未被说明的字母.

示例：

奇数集：{x|x=2n+1, n∈N}.

偶数集：{x|x=2n, n∈N}.

子集

描述 A 真包含于 B 的 Venn 图

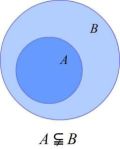
如果集合 A 的每一个元素都是集合 B 的元素，就称 A 是 B 的一个子集.

记作 A⊆B（读作：A 包含于 B）或 B⊇A（B 包含 A）.

如果 A⊆B 并且 B⊆A，就说这两个集合相等，记作：A=B.

如果 A⊆B 但是 B≠A，就说 A 是 B 的真子集，记作：A⫋B，读作：A 真包含于 B. 例如，(1, 6)⫋[1, 6].

包含关系还有传递性：若 A⊆B，B⊆C，则 A⊆C；若 A⫋B，B⊆C，则 A⫋C；等等.